区块链加密算法介绍
入门
区块链提供了通过机器算法解决参与人之间的信任问题的全新方案,其核心的核心就是在不完全信任的各方,通过深度使用密码学算法来保证数据的不可篡改特性。
比特币,谁能动我的钱
比特币是公有链,账本分布在无中心的节点上,任何一个节点都可以发出一个转让比特币的交易。那我的比特币是如何保证不被别人转走的呢?
假设你拥有100比特币,那么在公开账本上存有一个数据结构,即所谓的UTXO,其主要内容有:
▲ index: 索引
▲ value: 金额
▲ hash:一个SHA256的数据摘要
▲ script: 脚本,这个是重点要讲的
这个script是一串可执行的二进制代码,比特币定义了一个基于堆栈的脚本执行器,可以执行加减乘除、移位、HASH、验签等算法,类似于常见的科学计算器。当你想花费持有的比特币时,首先需要执行作为输入交易对应UTXO的脚本(script),称之为“解锁脚本”,只有执行成功才能继续。
最常用的一个解锁脚本就是P2PKH脚本:
OP DUP OF HASH160 < Public Key Hash > OP EQUAL
解锁时传入签名和公钥组成完整脚本:
<Signature> <Public Key> OP DUP OP Hash160 < Public key
翻译起来就是: “公钥的HASH160等于<脚本里面的值>,并且用这个公钥对HASH值验证签名能够通过”。计算通过,才可以花费这笔资金。
因为私钥保存在你自己手上,其他人无法计算出一个满足条件的签名,从而保证了这笔资金只有你自己可以使用。
这里除了数字签名外,还有一点体现了中本聪真的很聪明,账本上不会存储你的公钥,而是其HASH160(双HASH,SHA256+RIPEMD160),由于HASH是单向的,从HASH无法反向推导公钥,这样大大减少未来量子机会带来的风险。
HASH链之如何防止篡改
前面讲了数字签名在比特币的用法,这里结合区块链数据结构本身讲一下HASH的用法。
一个块只是组织数据的结构,这里暂不详述,关键是块里面有个重要的参数,前一块的HASH,这样就形成一个链式结构。
我们把数据竖起来看,就像是玩积木游戏,节点你一块我一块向上罗,每一块和前一块都有个钩子。如果这个时候有人试图篡改之前的一笔交易,势必会导致那个块的HASH变了,那为了使得改过的交易被大家认可,他可以以这个被改过的块为起点,重新计算后面所有的块,关键是还得比拼得过全世界其他的节点,目前还没人能够做到。
这里就突出了HASH算法的特点:
▲数据改变一点点,HASH改变非常大。
▲无法给不同的数据计算出相同的HASH(或者说非常难)。
比特币和以太坊的公私钥—ECC算法
RSA又慢又不安全,所以比特币和以太坊都不采用,而是使用了更安全的椭圆曲线算法 – ECC来做非对称加密基础算法。ECC的210位算法难度就相当于RSA 2048的难度,性能则是数量级的区别。那么椭圆算法又是何方神圣呢?
前面讲过非对称算法无非是设计一个数学难题,使得单向计算很方便,而反向计算很难,如RSA使用因式分解的原理,两个大质数相乘很容易,但大数分解质因子很难。
椭圆算法ECC其实就是利用乘法容易,而除法难的特点,设计一个乘法:K = k * G,其中大K是公钥,小k是私钥,G是生成点。由私钥推导公钥很容易,只需要k个G相加即可。但是从公钥推导私钥很难,也就是无法计算公钥K除以G。
当然这个加法不能用我们日常的整数加减法,而是利用函数所定义的一个特殊椭圆曲线上散列点的特性定义的加法。其中p是一个常数。不同p可以设计成不同的曲线,比特币使用的p = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1,这个曲线的名称就叫secp256k1。这是一个非常大的数,曲线上的点是一个复杂散点,为了方便展示,这里用小很多的17阶曲线表示加法的定义:
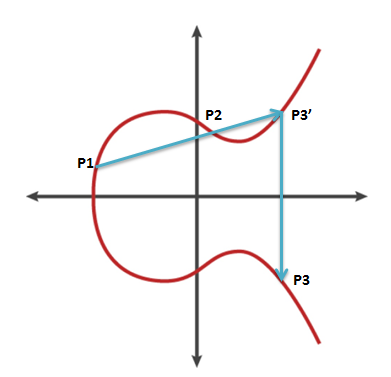
加法定义就是曲线上任意两个点P1和P2,必有第三个点P3,是P1和P2连线的延长线与曲线相交点的x轴映射的点,定义P1+P2=P3。通过数学算法可以证明这种点满足加法乘法交换律:
▲ A + B +C = A + (B + C)
▲ A(B+C) = AB + A*C
暂且不进行证明赘述,需要说明的是这里为了完善计算还定义了无穷远点O(相当于0),满足:P1 + O = P1。(思考一下:如果P1 + P2 = O,那么P1 = -P2了吗?)
ECC加密过程:
▲ K = k G, 大K是公钥,小k是私钥;
▲ 把明文编码成曲线上的点M;
▲ 生成一个随机数r;
▲ 计算密文C1=M + rK, C2 = r*G,其中大K是公钥;
▲ 对方收到密文后,可以计算C1 - kC2 = M,其中小k是私钥;
▲ 攻击者得到C1、 C2,公钥K以及基点G,没有私钥是无法计算出M的。
ECC算法用很短的密钥就能达到RSA2048的安全强度,而且计算速度有数量级的提高,所以目前应用很普遍,国密中的SM2就是基于ECC算法的。
隐私保护
由于区块链是在非完全信任的一组参与人之间,通过算法解决信任问题,之前讲述的算法保证了数据不可篡改,只有自己才可以操作自己的数据,但是还欠缺一个很重要的课题 – 隐私。
隐私和不可篡改其实有些相互矛盾,要实现不可篡改,就得让其他人来验证数据,比如公有链是全网用户都来验证;但是隐私又想只有授权的人才可以验证,甚至希望其他人能验证但是不知道数据,比如盲签名、同态算法等。本节讲述在非安全环境下处理安全数据的一些方法。
数字信封
用非对称算法可以把机密信息安全传给指定的接收人,通常我们会使用对方的公钥进行加密,同时使用自己的私钥对数据进行签名。数字信封提供了一个更方便强大的方法,使得信息只有特定的接收人才可以阅读。
数字信封的功能类似于普通信封,内容被包起来,上面写了接收人,只有接收人才能拆信。
制作信封方法:
▲准备一个生成器
CMSEnvelopedDataGenerator edGen = new CMSEnvelopedDataGenerator();
▲添加接收人:
edGen.addRecipientinfoGenerator(<接收人>)
接收人可以是公钥证书、普通公钥或者密码,可以有多个。
▲制作信封
edGen.generate(<内容>,<加密器>);
拆信封时,只要凭自己的公钥找到自己的收件人信息,然后用持有的私钥抽取内容即可。
组签名和环签名
通常一个合同是以公司的名义进行签署的,例如公司A有三个合同经办人C1、C2、C3,均可以代表公司签署合同。
这里有几个要求:
▲ 所签署的合同使用公司的公钥可以验证确实是公司所签署;
▲ 能够进一步确定合同经办人的身份;
▲ 经办人如离职被吊销个人证书,不影响已有业务数据。
按照孙子定理,n个整数(公钥)的同余方程组是有唯一解的,那么理论上根据组员公钥集合{K1, K2, ..., Kn}选择一组模M,可以求解x做组因子, 实现组员使用自己的私钥ki和x可以对密文进行解密 D(ki, x, C) = P。
类似的原理可以应用到数字签名,实现:
▲ 群组签名:机构使用群组公钥做自己的公钥,可以通过验证签名确定签名属于指定的机构,而机构管理员可以进一步确定是那个成员签署的。
▲ 环签名:对于匿名要求,可以确定签名是来自于一个群组的成员,但是无法确定是具体哪个成员签署的。
同态加密
私密数据的处理通常是在组内进行,但是使用区块链技术后,私密数据的处理可能会需要在无中心的节点上,甚至是第三方的节点进行处理。这时就需要把要处理的数据在保密状态下进行。
例如股东A有100股,卖出60股剩余40股,这是一个减法操作。如果这个过程在智能合约中,智能合约又运行在多个非完全信任的节点上,如果需要将真实股份数量加密,则需要实现一个减法同态:
C3 = C1 - C2, 其中C1,2,3均是密文,执行减法的节点无法知道实际余额和发生额,但是股东A可以使用自己的密钥解密 D(C3) = P = P1-P2, 其中P表示明文,D表示解密算法。
目前已实现的算法主要有:
▲ Paillier方案
概率公钥加密,基于复合剩余类的困难问题。满足加法和数乘同态。
▲ BGV和RLWE方案
BGV和RLWE都是基于LWE(Learning With Errors)难题的同态算法, 支持加法、乘法、减法和移位运算的同态。源码在github上开源- HElib。
▲ 基于其他数学难题的方案
如基于决断问题等。
全同态算法虽然实现已经取得很大进展,但其实现效率还远未达到实用要求。
