什么是原码、反码、补码
os数字在自然界中抽象出来的时候,一棵树,两只猪,是没有正数和负数的概念的
计算机保存最原始的数字,也是没有正和负的数字,叫没符号数字
如果我们在内存分配4位(bit)去存放无符号数字,是下面这样子的:
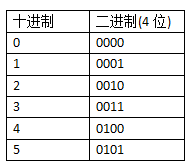
后来在生活中为了表示“欠别人钱”这个概念,就从无符号数中,划分出了“正数”和“负数”
正如上帝一挥手,从混沌中划分了“白天”与“黑夜”
为了表示正与负,人们发明了"原码",把生活应该有的正负概念,原原本本的表示出来
把左边第一位腾出位置,存放符号,正用0来表示,负用1来表示:
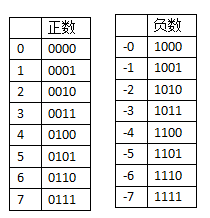
但使用“原码”储存的方式,方便了看的人类,却苦了计算机
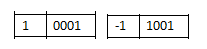
我们希望 (+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)
这不是我们想要的结果
另外一个问题,这里有一个(+0)和(-0)
为了解决“正负相加等于0”的问题,在“原码”的基础上,人们发明了“反码”
“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反:
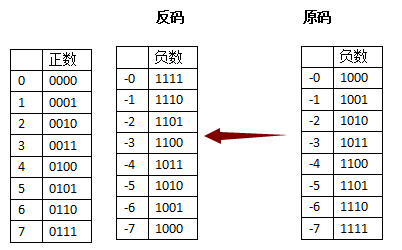
当“原码”变成“反码”时,完美的解决了“正负相加等于0”的问题
过去的(+1)和(-1)相加,变成了0001+1110=1111,刚好反码表示方式中,1111象征-0
人们总是进益求精,历史遗留下来的问题:
- 有两个零存在,+0
- -0
我们希望只有一个0
所以发明了"补码",同样是针对"负数"做处理的"补码"的意思是,从原来"反码"的基础上,补充一个新的代码,(+1)我们的目标是,没有(-0)
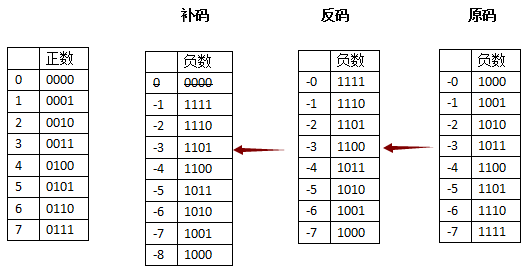
有得必有失,在补一位1的时候,要丢掉最高位
我们要处理"反码"中的"-0",当1111再补上一个1之后,变成了10000,丢掉最高位就是0000,刚好和左边正数的0,完美融合掉了
这样就解决了+0和-0同时存在的问题
另外"正负数相加等于0"的问题,同样得到满足
举例,3和(-3)相加,0011 + 1101 =10000,丢掉最高位,就是0000(0)
同样有失必有得,我们失去了(-0) , 收获了(-8)
以上就是"补码"的存在方式
结论:保存正负数,不断改进方案后,选择了最好的"补码"方案
