循环神经网络(具有记忆功能的网络)- Tensorflow
循环神经网络
TensorFlow循环神经网络
循环神经网络( recurτent neural network,RNN)源自于 1982 年由 Saratha Sathasivam 提出的霍普菲尔德网络。因为实现困难,在其提出时并且没有被合适地应用。该网络结构也于1986年后被全连接神经网络以及一些传统的机器学习算法所取代。然而,传统的机器学习算法非常依赖于人工提取的特征,使得基于传统机器学习的图像识别、 语音识别以及自然语言处理等问题存在特征提取的瓶颈。而基于全连接神经网络的方法也存在参数太多、无法利用数据中时间序列信息等问题。
前面讲的内容可以理解为静态数据的处理,也就是样本是单次的,彼此之间没有关系。然而人工智能对计算机的要求不仅仅是单次的运算,还需要让计算机像人一样具有记忆功能。循环神经网络(RNN),它是一个具有记忆功能的网络。这种网络最适合解决连续序列的问题,善于从具有一定顺序意义的样本与样本间学习规律。
循环神经网络的主要用途是处理和预测序列数据。在之前介绍的全连接神经网络或卷积神经网络模型中,网络结构都是从输入层到隐含层再到输出层,层与层之间是全连接或部分连接的,但每层之间的节点是无连接的。考虑这样一个问题,如果要预测句子的下一个单词是什么, 一般需要用到当前单词以及前面的单词,因为句子中前后单词并不是独立的。
比如,当前单词是“很”,前一个单词是“天空”,那么下一个单词很大概率是“蓝”。循环神经网络的来源就是为了刻画一个序列当前的输出与之前信息的关系。从网络结构上,循环神经网络会记忆之前的信息,并利用之前的信息影响后面结点的输出。也就是说,循环神经网络的隐藏层之间的结点是有连接的 ,隐藏层的输入不仅包括输入层的输出 ,还包括上一个时刻隐藏层的输出 。
特点、优点
优点:模型具备记忆性。
缺点:不能记忆太前或者太后的内容,因为存在梯度爆炸或者梯度消失。
了解RNN的工作原理
开始之前,我们先看看人脑是怎么处理的。
了解人的记忆原理
如果你身边有2、3岁的小孩子的话,可以仔细观察一下,他说话时虽然能表达出具体的意思,但是听起来总会觉得怪怪的。在刚开始说话时,把“我要”说成了“要我”,一看到喜欢吃的小零食,就会用手指着小零食对你大喊“要我,要我……”。
类似这样的话为什么我们听起来会感觉很别扭呢?这是因为我们的大脑受刺激时对一串后续的字有预测功能。如果从神经网络的角度来理解,大脑中的语音模型在某一场景下一定是对这两个字有先后顺序区分的。比如,第一个字是“我”,后面跟着“要”,人们就会觉得正常,而使用“要我”,来匹配“我要”的意思在生活中很少遇到,于是人们就会觉得很奇怪。
当获得“我来找你玩游”信息后,大脑的语言模型会自动预测后一个字为“戏”,而不是“乐、泳”等其他字
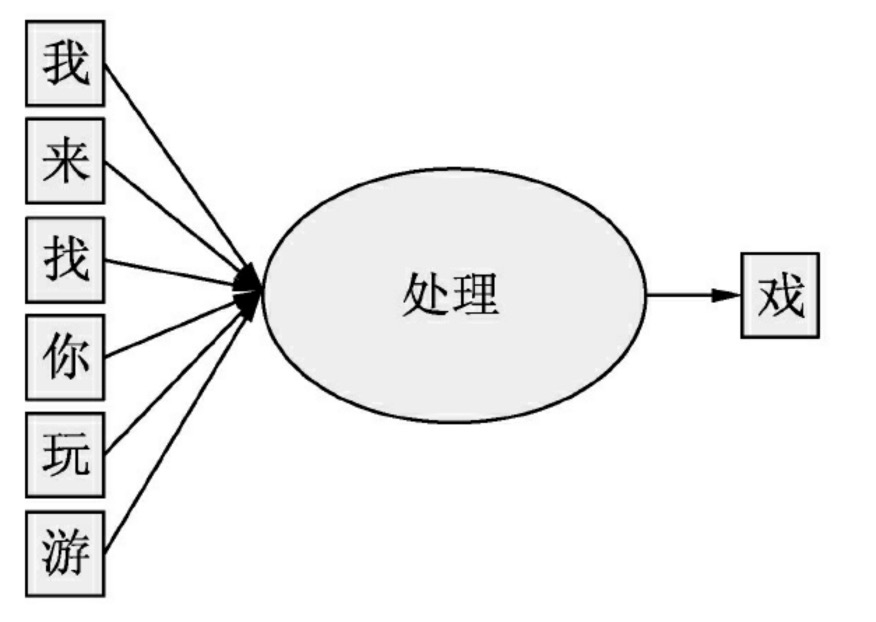
图中的逻辑并不是在说完“我来找你玩游”之后进入大脑来处理的,而是每个字都在脑子里进行着处理,将图中的每个字分别裁开,在语言模型中就形成了一个循环神经网络,图中的逻辑可以用下面的伪码表示:
(input我 + empty—input)→ output我
(input来 + output我)→ output来
(input找 + output来)→ output找
(input你 + output找)→ output你
……
这样,每个预测的结果都会放到下一个输入里进行运算,与下一次的输入一起来生成下一次的结果。
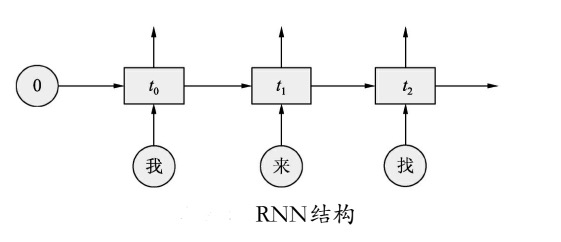
上图也可以看成是一个链式的结构,如何理解链式结构呢?举个例子:当小孩上了幼儿园,学习了《三字经》,而且可以背很长的内容,背得很熟练,于是我想考考他,就问了一个中间的句子“名俱扬”下一句是啥,他很快说了出来,马上又问他上一句是啥,他想了半天,从头背了一遍,背到“名俱扬”时才知道上一句是“教五子”。
这种现象可以理解为我们大脑并不是简单的存储,而是链式的、有顺序的存储。这种“链式的、有顺序存储”很节省空间,对于中间状态的序列,我们的大脑没有选择直接记住,而是存储计算方法。当我们需要取值时,直接将具体的数据输入,通过计算得出来相应的结果。这种解决方法在很多具体问题时都会用到。
例如:程序员常常会使用一个递归的函数来求阶乘n!=n×(n-1)×……1。
函数的代码如下:
long ff(int n) {
long f;
if(n<0) printf("n<0,input error");
else if(n==0||n==1) f=1;
else f=ff(n-1)*n;
return(f);
}
还有,我们在计算加法时的进位过程。23+17的加法过程是:先个位加个位,再算十位加十位;然后将个位的结果状态(是否有进位)送到十位的运算中去,则十位是2+1+个位的进位数(1)等于4。
RNN的应用领域
对于序列化的特征的任务,都适合采用RNN网络来解决。细分起来可以有情感分析(Sentiment Analysis)、关键字提取(Key TermExtraction)、语音识别(Speech Recognition)、机器翻译(Machine Translation)和股票分析等。
正向传播过程
A代表网络,xt代表t时刻输入的x,ht代表网络生成的结果,A中间又画出了一条线指向自己,是表明上一时刻的输出接着输入到了A里面。
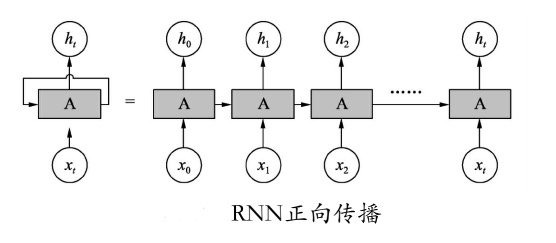
当有一系列的x输入到上图左侧结构中后,展开就变成了右侧的样子,其实就是一个含有隐藏层的网络,只不过隐藏层的输出变成了两份,一份传到下一个节点,另一份传给本身节点。其时序图如图所示
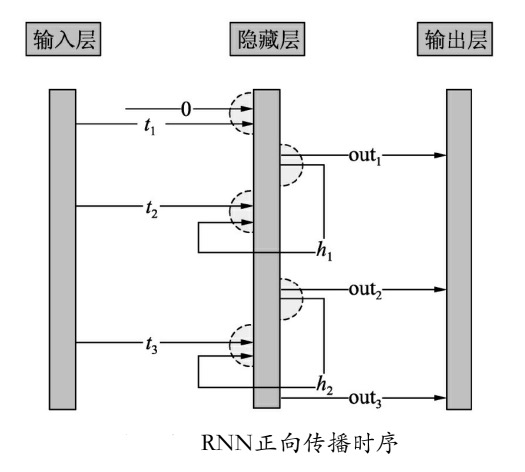
如上图所示,假设有3个时序t1 、t2 、t3,在RNN中可以分解成以下3个步骤。
- 开始时t1 通过自己的输入权重和0作为输入,生成了
out1。 - out1 通过自己的权重生成了h1 ,然后和t2 经过输入权重转化后一起作为输入,生成了out2 。
- out2 通过同样的隐藏层权重生成了h2,然后和t3 经过输入权重转化后一起作为输入,生成了out2 。
随时间反向传播
与单神经元相似,RNN也需要反向传播误差来调整自己的参数。RNN网络使用随时间反向传播(BackPropagation Through Time,BPTT)的链式求导算法来反向传播误差。
先来回顾一下反向传播的BP算法,如图所示。
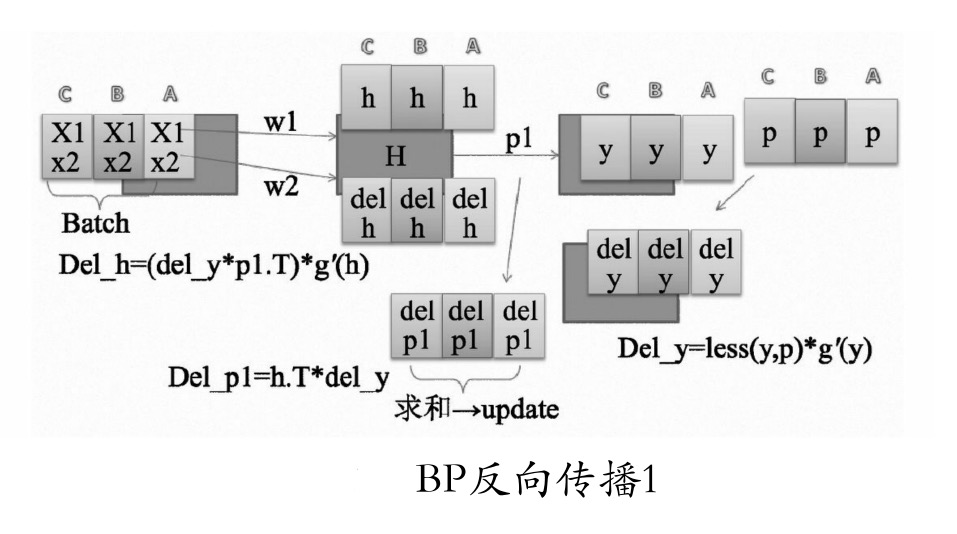
这是一个含有一个隐藏层的网络结构。隐藏层只有一个节点。具体的过程如下:
- 有一个批次含有3个数据A、B、C,批次中每个样本有两个数(x1、x2)通过权重(w1、w2)来到隐藏层H并生成批次h,如图中w1、w2两条直线所在方向。
- 该批次的h通过隐藏层权重p1生成最终的输出结果y。
- y与最终的标签p比较,生成输出层误差less(y,p)。
- less(y,p)与生成y的导数相乘,得到Del_y。Del_y为输出层所需要的修改值。
- 将h的转置与del_y相乘得到del_p1。这是源于h与p1相等得到的y,见第(2)步。
- 最终将该批次的del_p1求和并更新到p1上。
- 同理,再将误差反向传递到上一层:计算Del_h。得到
Del_h后再计算del_w1、del_w2并更新。
如果BP的算法您已经理解了,下面再来比较一下BPTT算法,如图所示。
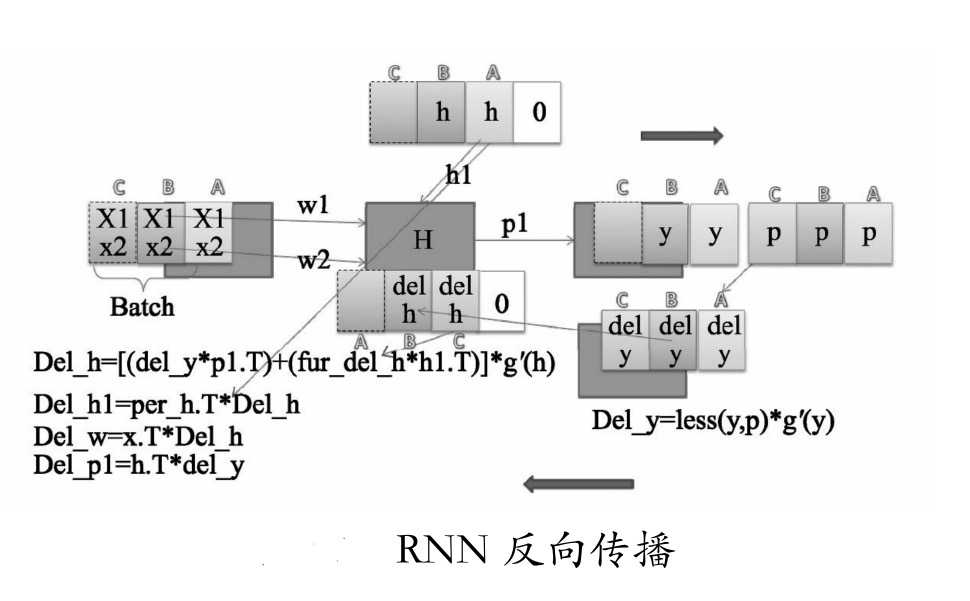
图中,同样是一个批次的数据A、B、C,按顺序进入循环神经网络。正向传播的实例是B正在进入神经网络的过程,可以看到A的h参与进来并一起经过P1生成了B的y。因为C还没有进入,为了清晰,这里用灰色表示。
当所有块都进入之后,会将p标签与输出进行Del_y的运算,由于C块的y是最后生成的,所以我们先从C块开始对h的输出传递误差Del_h。
图中的反向传播是表示C块已经反向传播完成,开始B块反向传播的状态,可以看到B块Del_h是由B块的del_y和C块的del_h通过计算得来的。这就是与BP算法不同的地方(BP中Del_h直接与自己的Del_y相关,不会与其他的值有联系)。
作为一个批次的数据,正向传播时是沿着ABC的顺序,当反向传播时,就按照正向传播的相反顺序,即每个节点的CBA挨个计算并传递梯度.
