使用隐藏层解决非线性问题 - Tensorflow
TensorFlow神经网络
多层神经网络非常好理解,就是在输入和输出中间多加些神经元,每一层可以加多个,也可以加很多层。下面通过一个例子将前面的异或数据进行分类。
实例:使用带隐藏层的神经网络拟合异或操作
实例描述
通过构建符合异或规律的数据集作为模拟样本,构建一个简单的多层神经网络来拟合其样本特征完成分类任务。
1.数据集介绍
所谓的“异或数据”是来源于异或操作,如图
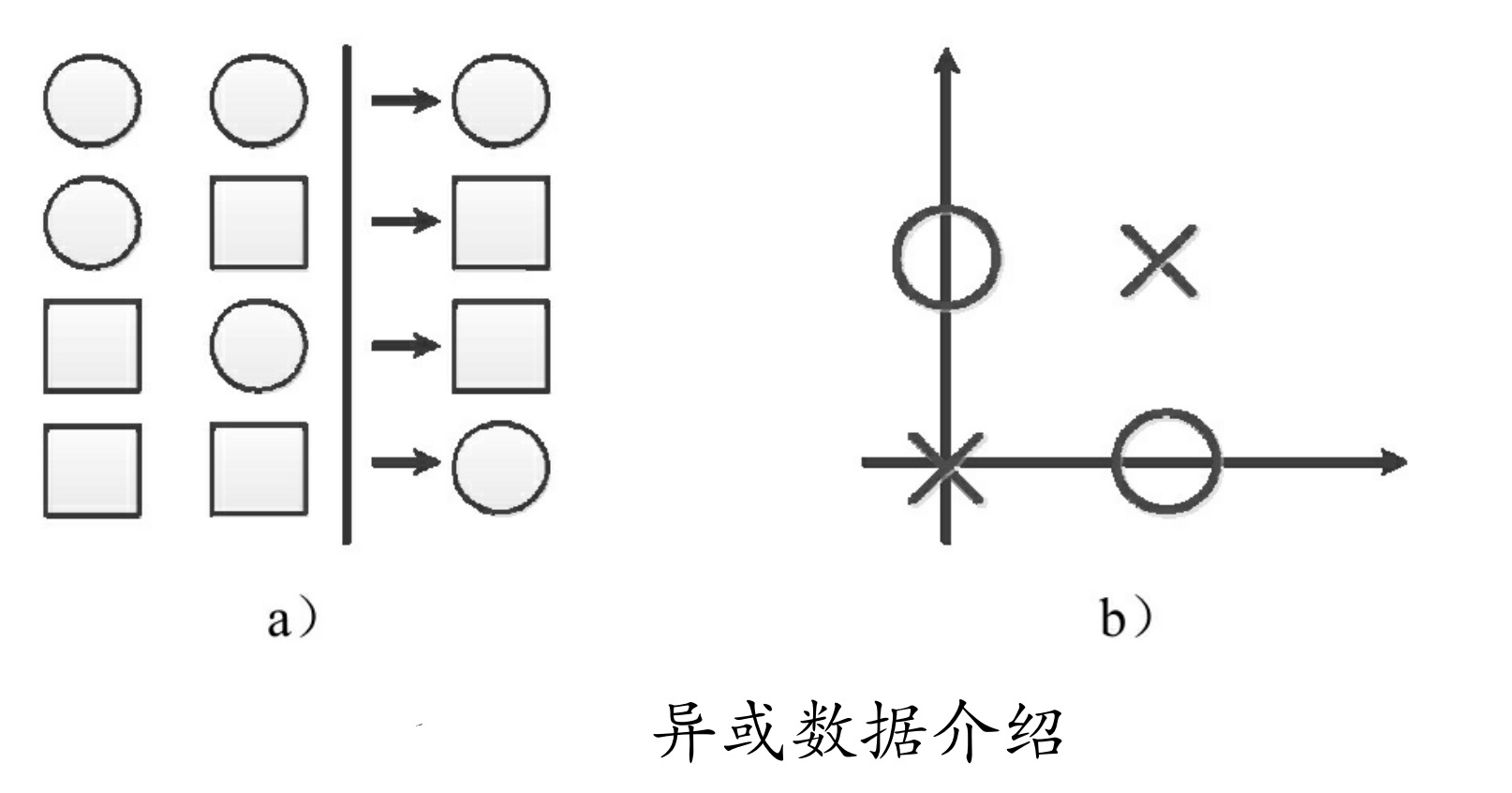
如图所示,a为0、1操作,b为数据在直角坐标系上的展示。
从a中可以看出,当两个数相同时,输出为0,不相同时输出为1,这就是异或的规则。表示为两类数据就是(0,0)和(1,1)为一类,(0,1)和(1,0)为一类。
2.网络模型介绍
本例中使用了一个隐藏层来解决这个问题
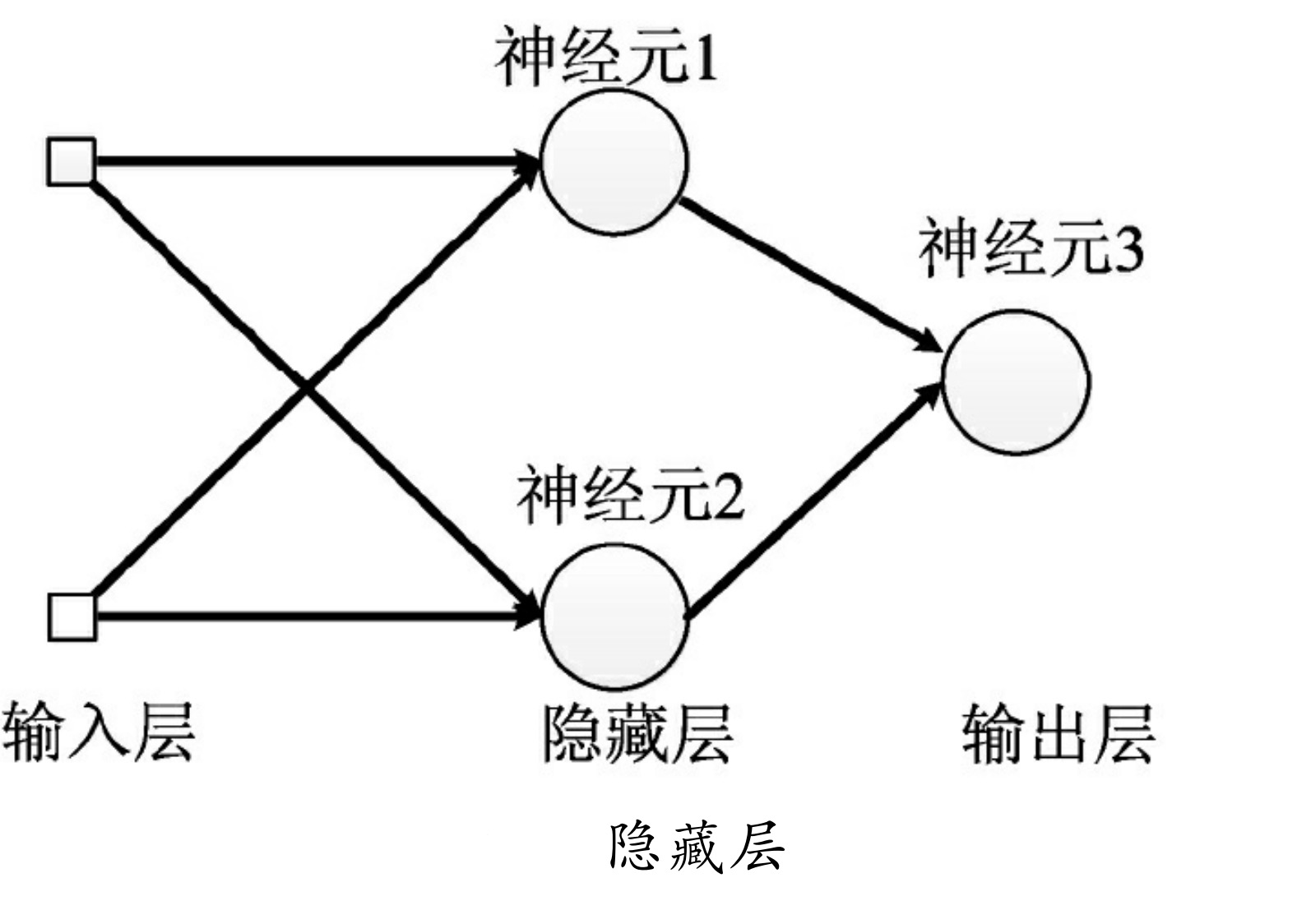
如图所示为要实现的网络结构。
3.定义变量
下面开始编写代码。第一步定义变量,在网络参数的定义中,输入是“2”代表两个数,输出是“1”代表最终的结果,再放一个隐藏层,该隐藏层里有两个节点。输入占位符为x,输出为y,学习率为0.0001。
代码7-3 异或操作
import tensorflow as tf
import numpy as np
learning_rate = 1e-4 # 0.0001
n_input = 2 # 输入层节点个数
n_label = 1 # 最终的结果
n_hidden = 2 # 隐藏层节点个数
x = tf.placeholder(tf.float32, [None,n_input])
y = tf.placeholder(tf.float32, [None, n_label])
4.定义学习参数
这里以字典的方式定义权重w和b,里面的h1代表隐藏层,h2代表最终的输出层。
代码7-3 异或操作(续)
weights = {
'h1': tf.Variable(tf.truncated_normal([n_input, n_hidden],stddev=0.1)),
'h2': tf.Variable(tf. truncated_normal ([n_hidden, n_label],stddev=0.1))
}
biases = {
'h1': tf.Variable(tf.zeros([n_hidden])),
'h2': tf.Variable(tf.zeros([n_label]))
}
5.定义网络模型
该例中模型的正向结构入口为x,经过与第一层的w相乘再加上b,通过Relu函数(大于0的留下,否则一律为0)进行激活转化,最终生成layer_1,再将layer_1代入第二层,使用Tanh激活(-1~1)函数生成最终的输出y_pred。
代码7-3 异或操作(续)
layer_1 = tf.nn.relu(tf.add(tf.matmul(x, weights['h1']), biases['h1']))
y_pred = tf.nn.tanh(tf.add(tf.matmul(layer_1, weights['h2']),biases['h2']))
loss=tf.reduce_mean((y_pred-y)**2)
train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)
模型的反向使用均值平方差(即对预测值与真实值的差取平均值)计算loss,最终使用AdamOptimizer进行优化。
6.构建模拟数据
代码7-3 异或操作(续)
#生成数据
X=[[0,0],[0,1],[1,0],[1,1]]
Y=[[0],[1],[1],[0]]
X=np.array(X).astype('float32')
Y=np.array(Y).astype('int16')
手动建立X和Y数据集,形成对应的异或关系。
7.运行session,生成结果
首先通过迭代10000次,将模型训练出来,然后将做好的X数据集放进去生成结果,接着再生成第一层的结果。
代码7-3 异或操作(续)
# 加载session
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
# 训练
for i in range(10000):
sess.run(train_step,feed_dict={x:X,y:Y} )
# 计算预测值
print(sess.run(y_pred,feed_dict={x:X}))
# 输出:已训练100000次
# 查看隐藏层的输出
print(sess.run(layer_1,feed_dict={x:X}))
运行上面的程序,得到如下结果:
[[ 0.10773809]
[ 0.60417336]
[ 0.76470393]
[ 0.26959091]]
[[ 0.00000000e+00 2.32602470e-05]
[ 7.25074887e-01 0.00000000e+00]
[ 0.00000000e+00 9.64471161e-01]
[ 2.06250161e-01 1.69421546e-05]]
第一个是4行1列的数组,用四舍五入法来取值,与我们定义的输出Y完全吻合。
第二个为4行2列的数组,为隐藏层的输出。
非线性网络的可视化及其意义
接上例中的第二个输出是4行2列数组,其中第一列为隐藏层第一个节点的输出,第二列为隐藏层第二个节点的输出,将它们四舍五入取整显示如下:
[[ 0 0]
[ 1 0]
[ 0 1]
[ 0 0]]
可以很明显地看出,最后一层其实是对隐藏层的AND运算,因为最终结果为[0,1,1,0]。也可以理解成第一层将数据转化为线性可分的数据集,然后在输出层使用一个神经元将其分开。
1.隐藏层神经网络相当于线性可分的高维扩展
在几何空间里,两个点可以定位一条直线,两条直线可以定位一个平面,两个平面可以定位一个三维空间,两个三维空间可以定位更高维的空间……
在线性可分问题上也可以这样扩展,线性可分是在一个平面里,通过一条线来分类,那么同理,如果线所在的平面升级到了三维空间,则需要通过一个平面将问题分类。如图所示,把异或数据集的输入x1、x2当成平面的两个点,输出y当作三维空间里的z轴上的坐标,那么所绘制的图形就是这样的。

很明显,这样的数据集是很好分开的。图中,右面的比例尺指示的是纵坐标。0刻度往下,颜色由浅蓝逐渐变为深蓝;0刻度往上,颜色由浅红逐渐变为深红。作一个平行于底平面、高度为0的平面,即可将数据分开,如图中的虚平面。我们前面使用的隐藏层的两个节点,可以理解成定位中间平面的两条直线。其实,一个隐藏层的作用,就是将线性可分问题转化成平面可分问题。更多的隐藏层,就相当于转化成更高维度的空间可分问题。所以理论上通过升级空间可分的结构,是可以将任何问题分开的。
2.从逻辑门的角度来理解多层网络
对于多层网络,还可以通过逻辑门的角度来理解,如图7-13所示。将数据集映射到直角坐标系中,通过可视化图形可以看到,在直角坐标系中有两条直线将其分开,对于两条直线的结果,可以再通过神经网络构建一个逻辑运算,即可将它们融合在一起并产生最终想要的结果。
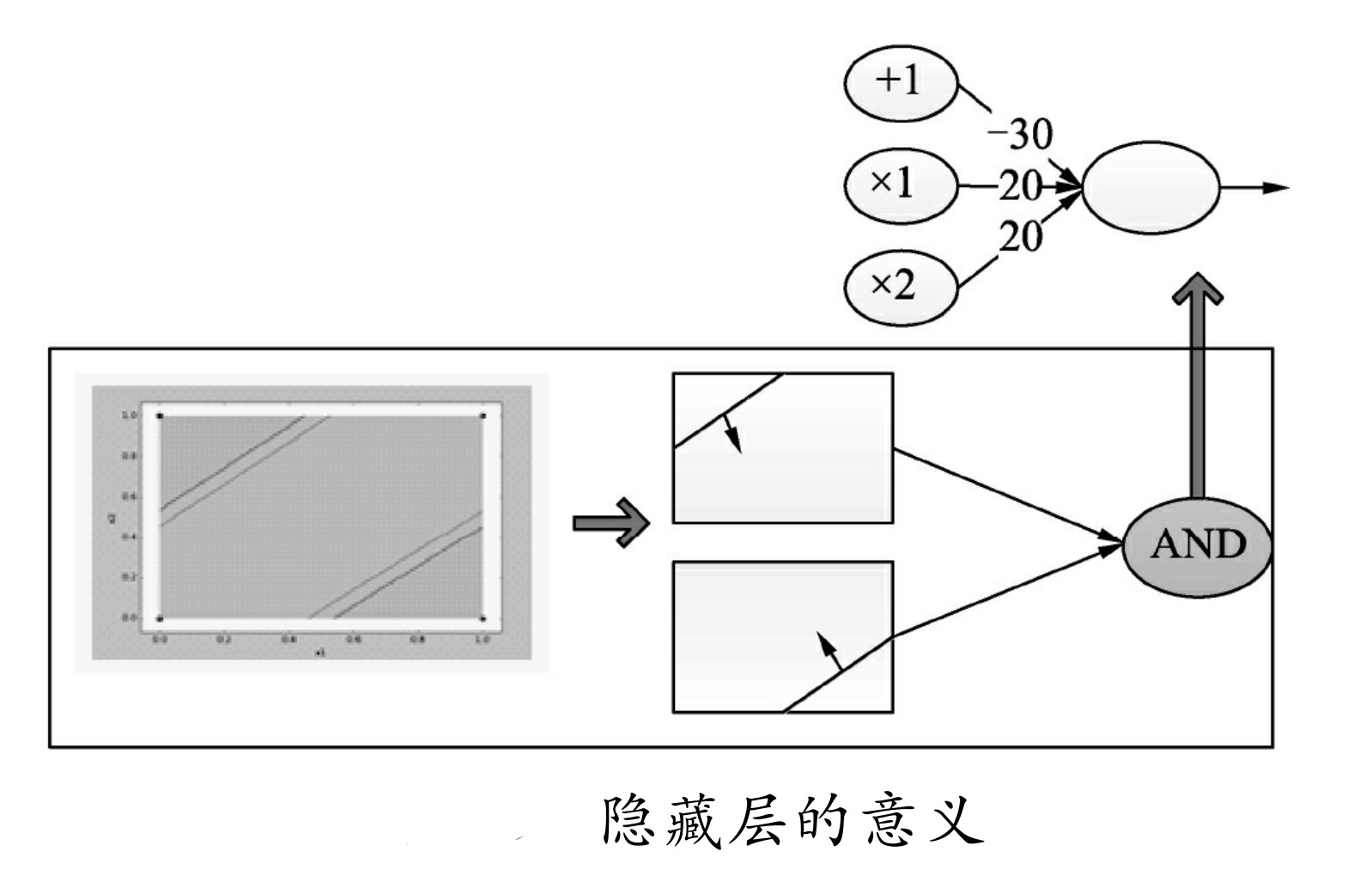
图中,对两条直线的结果取AND运算,即可实现异或的效果,而构建AND逻辑的权重很容易实现,图中使用w[-30,20],b[20]即实现了AND的逻辑。
类似这样的逻辑门还有很多,如图7-14中举例了神经元实现的AND、OR、NOT逻辑,最终通过这些逻辑门的运算,甚至不需要训练就可以搭建出一个异或的模型(如图所示部分)。
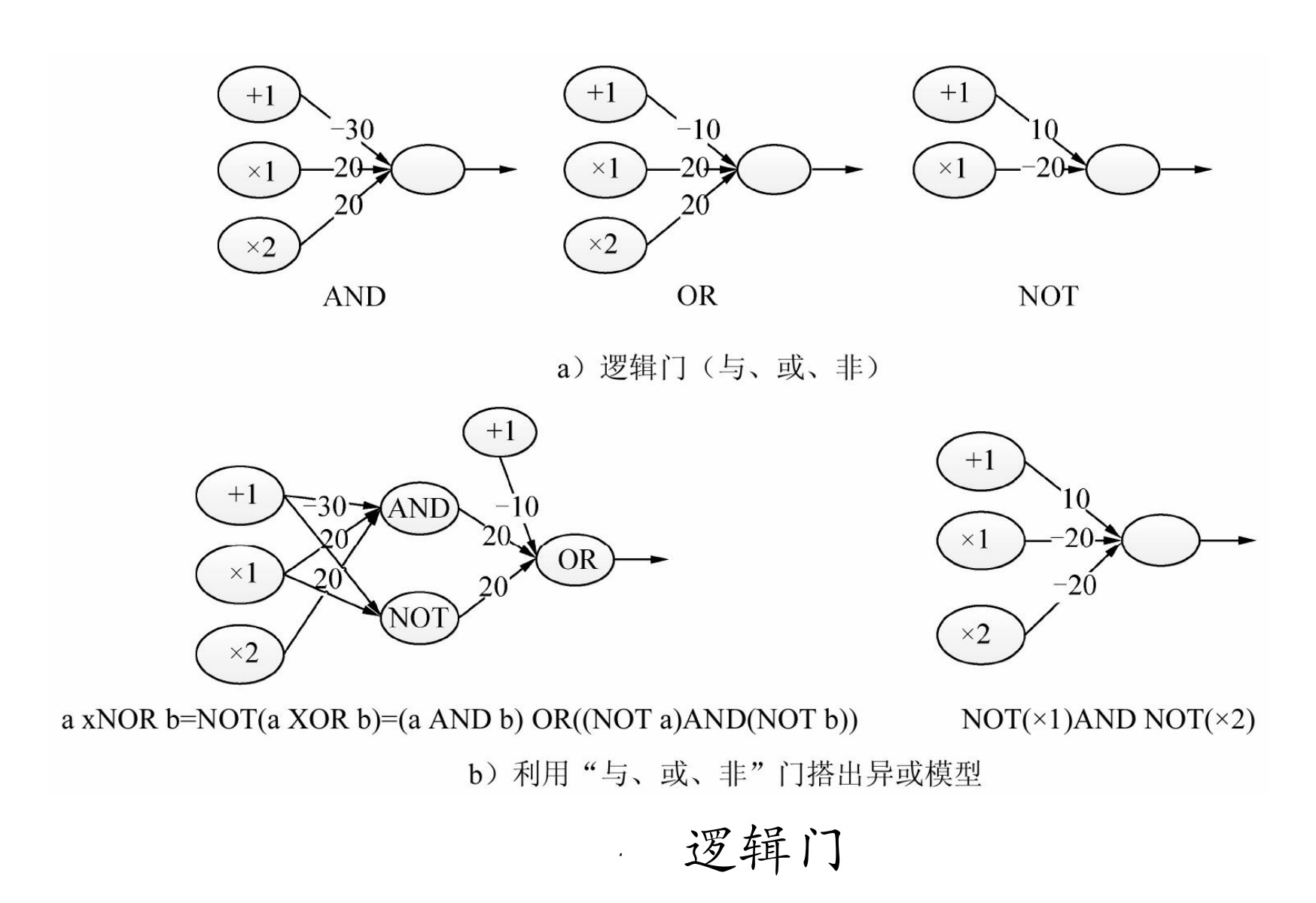
看到这里,了解计算机原理的读者都知道,CPU的基础运算都是在构建逻辑门基础之上完成的,例如,用逻辑门组成最基本的加减乘除四则运算,再用四则运算组成更复杂的功能操作,最终可以实现操作系统并在其上进行各种操作。
神经网络的结构和功能,使其具有编程和实现各种高级功能的能力,只不过这个编程不需要人脑通过学习算法来拟合现实,而是使用模型学习的方式,直接从现实的表象中优化成需要的结构。
所以说,这种多层的结构只要层数足够多,每层的节点足够多,参数合理,就可以拟合世界上的任何问题,而放在神经网络里考验的则是,模型的自学习功能是否足够高效和精准。
