numpy中np.dot()函数的用法
TensorFlow笔记
dot函数是对矩阵进行运算,返回的是两个数组的点积(dot product)
1、如果处理的是一维数组,则得到的是两数组的內积
In : d = np.arange(0,9)
Out: array([0, 1, 2, 3, 4, 5, 6, 7, 8])
In : e = d[::-1]
Out: array([8, 7, 6, 5, 4, 3, 2, 1, 0])
In : np.dot(d,e)
Out: 84
2、如果是二维数组(矩阵)之间的运算,则得到的是矩阵积(mastrix product)。
In : a = np.arange(1,5).reshape(2,2)
Out:
array([[1, 2],
[3, 4]])
In : b = np.arange(5,9).reshape(2,2)
Out: array([[5, 6],
[7, 8]])
In : np.dot(a,b)
Out:
array([[19, 22],
[43, 50]])
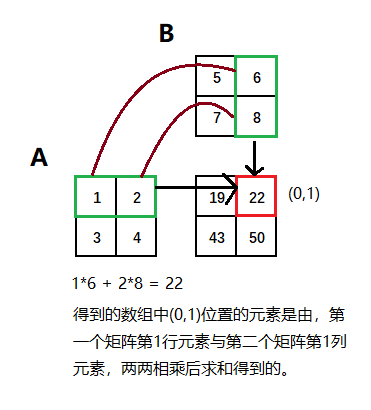
所得到的数组中的每个元素为,第一个矩阵中与该元素行号相同的元素与第二个矩阵与该元素列号相同的元素,两两相乘后再求和。
这句话有点难理解,但是这句话里面没有哪个字是多余的。结合下图理解这句话。
3、dot()函数可以通过numpy库调用,也可以由数组实例对象进行调用。
a.dot(b) 与 np.dot(a,b)效果相同。
注意:矩阵积计算不遵循交换律,
np.dot(a,b)和np.dot(b,a)得到的结果是不一样的。
