预测当天的股票价格 - tensorflow
TensorFlow循环神经网络
既然前面我们用预测股票来打比方,那么这里就演示一个预测股票的例子。直接修改实例72中的数据源即可。
实例描述
使用Seq2Seq模式对某个股票数据的训练学习,拟合特征,从而达到可以预测第二天股票价格的效果。
1、准备数据
需要准备一个股票的数据,本例中的格式是CSV,也可使用本书的配套例子中的数据“600000.csv”(笔者只是随意爬取了A股中的第一个股票,没有其他特殊意义),本书配套代码中提供了一个爬虫代码文件,见代码“9-31STOCKDATA.py”文件。
2、导入股票数据
直接在“9-30:基本seq2seq.py”文件基础上修改代码,添加载入股票函数loadstock,里面使用了pandas,所以要将该库导入进去。实例中将close收盘价格载入内存用于做样本生成。当然读者也可以自行修改字段,可以将开盘价、最高价格和最低价格等都载入内存作为样本数据,只需将对应的列名放入predictor_names数组中即可。
代码9-32 seq2seqstock
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
pd.options.mode.chained_assignment = None # default='warn'
def loadstock(window_size):
names = ['date',
'code',
'name',
'Close',
'top_price',
'low_price',
'opening_price',
'bef_price',
'floor_price',
'floor',
'exchange',
'Volume',
'amount',
'总市值',
'流通市值']
data = pd.read_csv('600000.csv', names=names, header=None, encoding="gbk")
# predictor_names = ["Close",'top_price',"low_price","opening_price"]
predictor_names = ["Close"]
training_features = np.asarray(data[predictor_names], dtype="float32")
kept_values = training_features[1000:]
X = []
Y = []
for i in range(len(kept_values) - window_size * 2): # x ;前window_size,y后window_size
X.append(kept_values[i:i + window_size])
Y.append(kept_values[i + window_size:i + window_size * 2])
X = np.reshape(X, [-1, window_size, len(predictor_names)])
Y = np.reshape(Y, [-1, window_size, len(predictor_names)])
print(np.shape(X))
return X, Y
3、生成样本
直接修改代码中生成样本的函数generatedata,和其对应的内部调用的do_generate x_y函数,代码如下。
代码9-32 seq2seqstock(续)
def generate_data(isTrain, batch_size):
# 用前40个样本来预测后40个样本
seq_length = 40
seq_length_test = 80
global Y_train
global X_train
global X_test
global Y_test
# 载入内存
if len(Y_train) == 0:
X, Y = loadstock(window_size=seq_length)
# X, Y = normalizestock(X, Y)
# Split 80-20:
X_train = X[:int(len(X) * 0.8)]
Y_train = Y[:int(len(Y) * 0.8)]
if len(Y_test) == 0:
X, Y = loadstock(window_size=seq_length_test)
# X, Y = normalizestock(X, Y)
# Split 80-20:
X_test = X[int(len(X) * 0.8):]
Y_test = Y[int(len(Y) * 0.8):]
if isTrain:
return do_generate_x_y(X_train, Y_train, batch_size)
else:
return do_generate_x_y(X_test, Y_test, batch_size)
def do_generate_x_y(X, Y, batch_size):
assert X.shape == Y.shape, (X.shape, Y.shape)
idxes = np.random.randint(X.shape[0], size=batch_size)
X_out = np.array(X[idxes]).transpose((1, 0, 2))
Y_out = np.array(Y[idxes]).transpose((1, 0, 2))
return X_out, Y_out
4、运行程序查看效果
由于股票数据没有固定的规则而言,并且数据量又较大,所以加大batch到100,加大迭代次数到100000,代码片段如下。
代码9-32 seq2seqstock(续)
……
seq_length = sample_now.shape[0]
batch_size = 100
output_dim = input_dim = sample_now.shape[-1]
hidden_dim = 12
layers_num = 2
# 学习率
learning_rate = 0.04
nb_iters = 100000
lambda_l2_reg = 0.003 # L2 regularization of weights - avoids overfitting
……
其他地方均不用变,直接运行代码即可,输出如图所示。
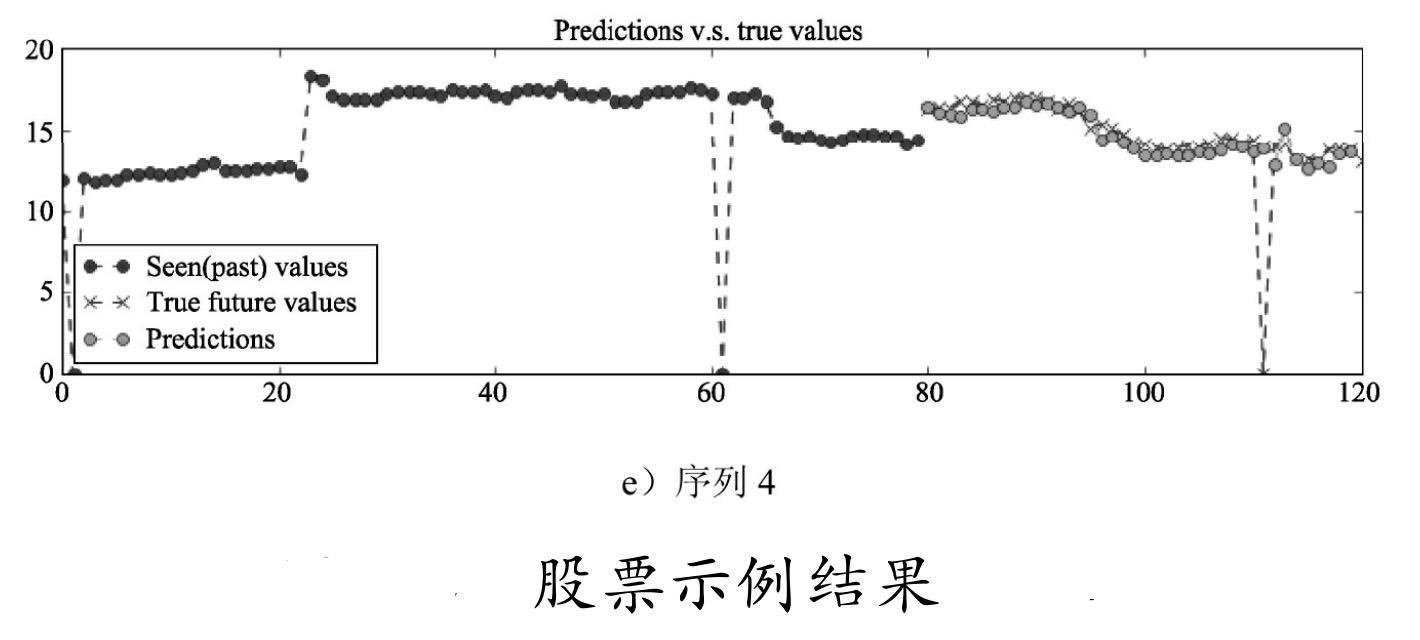
可见损失值还是比较高的,中间有两次还出现了飙升,由于没有对数据进行清洗和修正,所以会看到序列中有突然变为0的情况,这是由于或许当天是停牌或者数据缺失等情况照成的。恰好我们可以把它当成噪声数据来泛化网络。图9-30中序列80~120之间的点(即图中灰色的点)代表预测的结果,X代表真实的结果,可以看到,虽然不是很精确,但是总体还是与真实数据很接近的。在真实使用场景中,可以修改显示部分的测试代码,不用随机取样本数据,而是把最后一段时间序列取出来并放到模型里,输出的最后一个预测值即是当天的收盘价预测。
提示: 股市有风险,用机器炒股也要谨慎。这里演示的只是一个模型,其精确度和拟合度还有待提高,并不能当作炒股指导工具。
通过两个例子的练习,希望读者可以掌握Seq2Seq的基本使用。其实,这种简单的Seq2Seq框架在实际应用中对超长序列数据的学习效果并不是很好。这是因为无论输入端有多大变化,Encoder给出的都是一个固定维数的向量,存在信息损失,所以输入的序列越长,Encoder的输出丢失的原始信息就越多,传入Decoder后,很难在Decoder中有太多的特征表现。对于这个问题,引出了下面的基于注意力的Seq2Seq。
